2  Análisis Exploratorio

En esta primera sección se revisan herramientas básicas para un análisis descriptivo de datos espaciales.

Como en otros modelos estadísticos, un punto de partida es revisar sobre qué tipo de objeto probabilista se busca hacer inferencia. Es muy útil recordar primero la noción de proceso estocástico tal como se da en (Klenke 2020).

Definición 2.1 (Proceso estocástico) Sea \(I\subseteq\mathbb{R}\). Una familia de variables aleatorias \(Z={(Z_t)}_{t\in I}\), en un espacio de probabilidad \((\Omega,\mathcal{F},\mathbb{P})\), que toma valores en \((E,\mathcal{E})\), es un proceso estocástico con conjunto de tiempo \(I\) y espacio de estados \(E\).

Muchas de las técnicas para estudiar estos procesos que varían en el tiempo dependen de que \(I\) es un conjunto ordenado. Además, para cada \(\omega\in\Omega\), el mapeo \(t\mapsto Z_t(\omega)\) indica lo que hace el proceso a tiempo \(t\). A partir de esto, es inmediato extender la definición a un proceso espacial (o espacio-temporal).

Definición 2.2 (Proceso espacio-temporal) Sean \(I\subseteq\mathbb{R}\) y \(A\subseteq\mathbb{R}^d\). Una familia de variables aleatorias \(Z={(Z_{x,t})}_{(x,t)\in A\times I}\), en un espacio de probabilidad \((\Omega,\mathcal{F},\mathbb{P})\), que toma valores en \((E,\mathcal{E})\), es un proceso espacio-temporal en la región \(A\) con conjunto de tiempo \(I\) y espacio de estados \(E\).

En este texto se manejarán únicamente procesos espaciales, es decir, consideraremos que \(t\) es fijo. A una realización del proceso le denotaremos por \(z={(z(x))}_{x\in A}\). En el contexto del análisis estadístico, se consideran distintos tipos de datos (o realizaciones ed \(Z\)).

Definición 2.3 (Dato espacial) Un dato espacial es aquel que incluye, además de su valor (numérico, categórico, conteo, etc.), información de localización. Esta información puede ser en forma de coordenadas, ubicaciones discretas en una red o cualquier otra manera de localización.

2.1 Tipos de datos espaciales

A partir de la estructura de esta realización \(z\), se pueden considerar distintos tipos de datos espaciales. De manera no exhaustiva, a continuación se presentan algunos de estos tipos de datos.

2.1.1 Datos de área o en retícula

Si \(A\) es una unión numerable de unidades de área, decimos que la muestra \(z\) son datos de área o de retícula. Este tipo de estructuras es común en imágenes satelitales, en el análisis de suelos y algunos estudios experimentales en agricultura. También se encuentran las imágenes médicas y la teledetección. Los datos pueden representar toda la población (imagen completa) o una submuestra.

El énfasis en hablar de “unidades de área” tiene más sentido al considerar que un mapa con división territorial cumple con estas propiedades. Siguiendo a (Moraga 2023), a continuación se presentan un mapa del número de muertes repentinas de niños en cada condado de Carolina del Norte, EE.UU., en el año de 1974, reportado originalmente en (Pebesma 2022a).

library(sf)
library(mapview)
d <- st_read(system.file("shape/nc.shp", package = "sf"), quiet = TRUE)
mapview(d, zcol = "SID74")

En el anterior ejemplo, cada región del espacio es un condado. A continuación se presenta un mapa sobre la elevación de Luxemburgo, en el cual todas las regiones del mismo tamaño y están distribuidas de manera uniforme en el espacio, también tomado de (Moraga 2023).

library(terra)
d <- rast(system.file("ex/elev.tif", package = "terra"))
plot(d)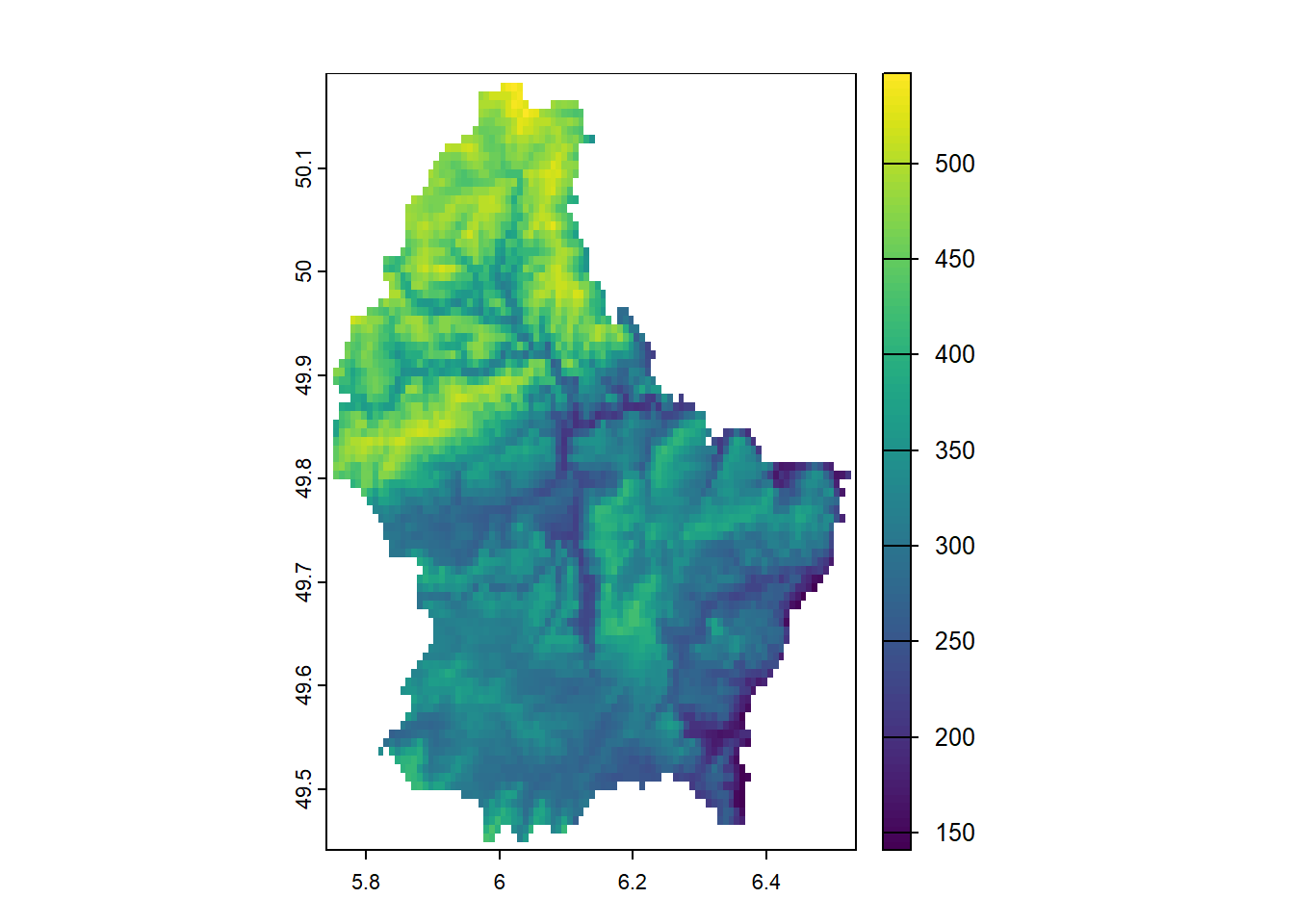

2.1.2 Datos geoestadísticos

Estos datos se miden de manera continua en el espacio, por lo que se consideran formas posiblemente irregulares. Una complicación de este tipo de datos es que normalmente sólo se dispone de observaciones en algunos puntos del espacio. Estos datos aparecen típicamente en cuestiones mineras, de ciencias del suelo, hidrológicas, meteorológicas u otros temas geológicos.

Como ejemplo, se muestra la distribución de plomo superficial en mg por kg de tierra, en un terreno muestreado tras una inundación del río Meuse en Países Bajos. Estos datos son de la librería sp de R.

library(sp)
library(sf)
library(mapview)

data(meuse)
meuse <- st_as_sf(meuse, coords = c("x", "y"), crs = 28992)
mapview(meuse, zcol = "lead",  map.types = "CartoDB.Voyager")

Este tipo de datos se obtienen con mediciones de infiltrómetros revisando la capacidad del suelo para absorber agua.

En este tipo de datos, las ubicaciones de muestreo son generalmente irregulares y se tiene como objetivo predecir la variable en ubicaciones no observadas. Esto se hace bajo la hipótesis de continuidad espacial del campo y que la correlación entre observaciones depende de la distancia.

2.1.3 Patrones puntuales

En este tipo de datos se centra el estudio en capítulos posteriores y en el caso de estudio. Aquí el dominio \(A\) se toma como aleatorio y las variables en \(Z\) sólo valen 1 o 0, indicando la ocurrencia o no de un evento. Estos patrones surgen de ubicar eventos, tales como aparición de enfermedades, nacimiento de especies, ubicación de viviendas, entre otros.

Como ejemplo, se presentan los datos de pinos de hoja larga en Georgia, los cuales se pueden encontrar en la biblioteca spatstat de R. Lo que se mide es la presencia de pinos con longitud de hoja mayor a cierto parámetro. El objetivo del estudio era ver si los árboles con estas características están distribuidos uniformemente al azar en la región o si se tiene algún tipo de agrupamiento o regularidad.

library(spatstat)

data(longleaf)

plot(longleaf, use.marks = FALSE, pch = 20, cex = 0.5, main = "Pinos de hoja larga en Georgia")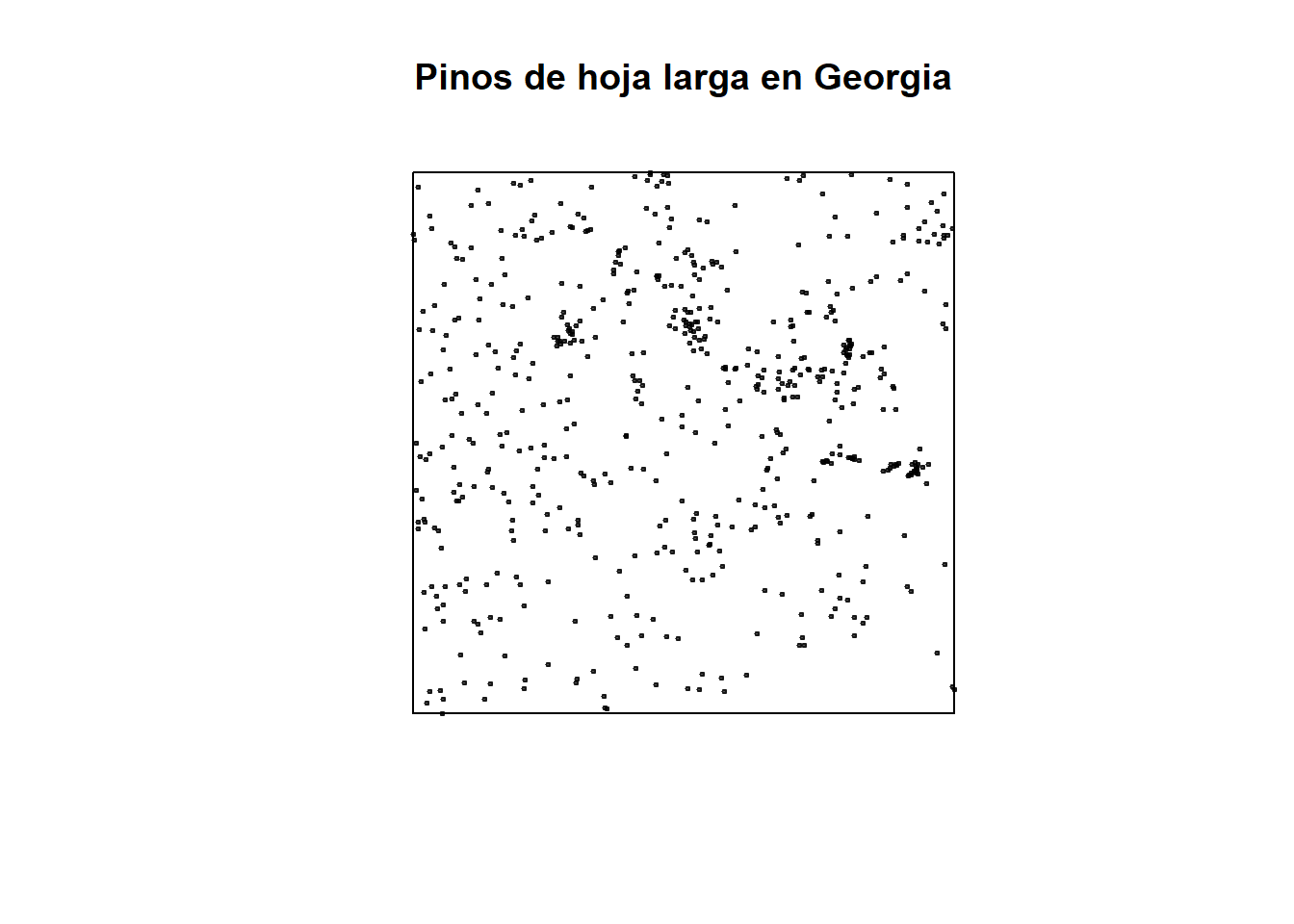

Se pueden considerar versiones más generales de este tipo de datos, como los datos puntuales marcados. En los datos puntuales marcados se considera que las observaciones pueden ser de distintos tipos dada alguna característica cualitativa.

La característica principal de este tipo de datos es que el interés está centrado en la posición de los eventos, ya que no hay variables medidas continuamente en el espacio.

2.2 Herramientas descriptivas

Para el caso de datos puntuales, es posible dar una noción de media y de varianza para datos en cualquier dimensión \(d\geq 1\).

Definición 2.4 (Centroide y dispersión de una muestra) Sean \(x=\{x_1,\ldots,x_n\}\subseteq\mathbb{R}^d\) puntos en el espacio, donde \(x_i=(x_i^{(1)},\ldots,x_i^{(d)})\), con \(i=1,\ldots,n\).

• El centroide espacial de \(x\) está dado por

\[\overline{x}=\frac{1}{n}\sum_{i=1}^nx_i=\left(\frac{1}{n}\sum_{i=1}^nx_i^{(1)},\ldots,\frac{1}{n}\sum_{i=1}^nx_i^{(d)}\right).\]

• La dispersión espacial de \(x\) está dada por

\[\sigma^2=\frac{1}{n}\sum_{i=1}^n{\|x_i-\overline{x}\|}^2,\]

donde \(\|\cdot\|\) es la norma euclidiana de \(\mathbb{R}^d\).

• La matriz de dispersión espacial de \(x\) está dada por

\[\Sigma=\frac{1}{n}\sum_{i=1}^n(x_i-\overline{x}){(x_i-\overline{x})}^T.\]

Para patrones de puntos más complejos como en el caso de los datos del río Meuse, se puede hablar de centros de masa ya que se considera que cada punto en el mapa tiene un valor asignado.

Definición 2.5 (Centroide de masa y dispersión de masa de una muestra) Sean \(x=\{x_1,\ldots,x_n\}\subseteq\mathbb{R}^d\) puntos en el espacio, donde \(x_i=(x_i^{(1)},\ldots,x_i^{(d)})\) con pesos \(w_i\neq 0\), con \(i=1,\ldots,n\).

• El centroide de masa espacial de \(x\) está dado por

\[\overline{x}_w=\frac{1}{W}\sum_{i=1}^nw_ix_i=\left(\frac{1}{n}\sum_{i=1}^nw_ix_i^{(1)},\ldots,\frac{1}{n}\sum_{i=1}^nw_ix_i^{(d)}\right)\quad\text{donde}\quad W=\sum_{i=1}^nw_i.\]

• La dispersión de masa espacial de \(x\) está dada por

\[\sigma^2_w=\frac{1}{W}\sum_{i=1}^nw_i{\|x_i-\overline{x}_w\|}^2,\]

donde \(\|\cdot\|\) es la norma euclidiana de \(\mathbb{R}^d\).

• La matriz de dispersión de masa espacial de \(x\) está dada por

\[\Sigma=\frac{1}{W}\sum_{i=1}^nw_i(x_i-\overline{x}_w){(x_i-\overline{x}_w)}^T.\]

Este tipo de estadísticos capturan no sólo dónde están los eventos, sino dónde se concentra el fenómeno. Siguiendo con los datos de Meuse, los centroides y las dispersiones para los datos de plomo se muestran a continuación.

library(sp)
library(sf)
library(mapview)
library(dplyr)

data(meuse)
meuse_sf <- st_as_sf(meuse, coords = c("x", "y"), crs = 28992)
coords <- st_coordinates(meuse_sf)
weights <- meuse_sf$lead

centroide <- colMeans(coords)
W <- sum(weights)
centro_masa <- colSums(weights * coords) / W

disp_espacial <- mean(rowSums((coords - centroide)^2))
disp_masa <- sum(weights * rowSums((coords - centro_masa)^2)) / W

p_centroide <- st_sf(tipo = "Centroide", geometry = st_sfc(st_point(centroide)), crs = 28992)
p_masa <- st_sf(tipo = "Centro de masa", geometry = st_sfc(st_point(centro_masa)), crs = 28992)

mapview(meuse_sf, zcol = "lead", map.types = "CartoDB.Voyager") +
  mapview(p_centroide, color = "blue", col.region = "blue", label = "Centroide") +
  mapview(p_masa, color = "red", col.region = "red", label = "Centro de masa")

library(knitr)
data.frame(
  Medida = c("Centroide X", "Centroide Y", "Centro de masa X", "Centro de masa Y",
             "Dispersión espacial", "Dispersión ponderada"),
  Valor = c(round(centroide[1], 1), round(centroide[2], 1),
            round(centro_masa[1], 1), round(centro_masa[2], 1),
            round(disp_espacial, 2), round(disp_masa, 2))
) %>%
  kable(caption = "Resumen de características espaciales de los datos.")

Resumen de características espaciales de los datos.

Medida	Valor
Centroide X	1.800046e+05
Centroide Y	3.316349e+05
Centro de masa X	1.799196e+05
Centro de masa Y	3.316878e+05
Dispersión espacial	2.284400e+10
Dispersión ponderada	2.278173e+10

Si se tratara con datos a una escala muy grande, digamos datos en los que los datos están distribuidos a lo largo de todo el continente americano, es necesario tomar consideraciones topológicas de curvatura y restricciones a estar sobre el mapa. Esto ya que con las definiciones dadas podría ser que los puntos ni siquiera estén sobre el mapa (basta tomar el polo norte y el polo sur para tener un ejemplo de esto).

2.2.1 Visualización de datos

Aunque las estadísticas anteriores sí capturan información relevante para los datos, se pierde mucha información sobre la estructura espacial del fenómeno. Existen diversos recursos gráficos para poder discutir sobre datos espaciales, algunos de éstos se presentan en las siguientes secciones. Más sobre éstos y otros tipos de representaciones gráficas de datos espaciales se pueden ver en (Bivand, Pebesma, y Gomez-Rubio 2013) y en (Baddeley, Rubak, y Turner 2015).

Mapa de símbolos proporcionales

Un mapa de símbolos proporcionales es un tipo de gráfico que representa la magnitud de una variable en ubicaciones puntuales mediante símbolos cuyo tamaño es proporcional al valor observado.

Otra manera de visualizar los datos de pinos de hoja larga de la sección Sección 2.1.3 es la siguiente

library(spatstat)

data(longleaf)

plot(longleaf, maxsize=15, main = "Pinos de hoja larga en Georgia con diámetro")

Los diámetros de los árboles no están a escala: la leyenda muestra los diámetros en centímetros.

Mapas de color

Muestra la densidad o intensidad de eventos sobre una superficie. Siguiendo el ejemplo de los pinos de hoja larga

library(spatstat)

data(longleaf)

A <- colourmap(heat.colors(128), range=range(marks(longleaf)))

plot(longleaf,  pch=21, bg=A, cex=1, main = "Pinos de hoja larga en Georgia con diámetro")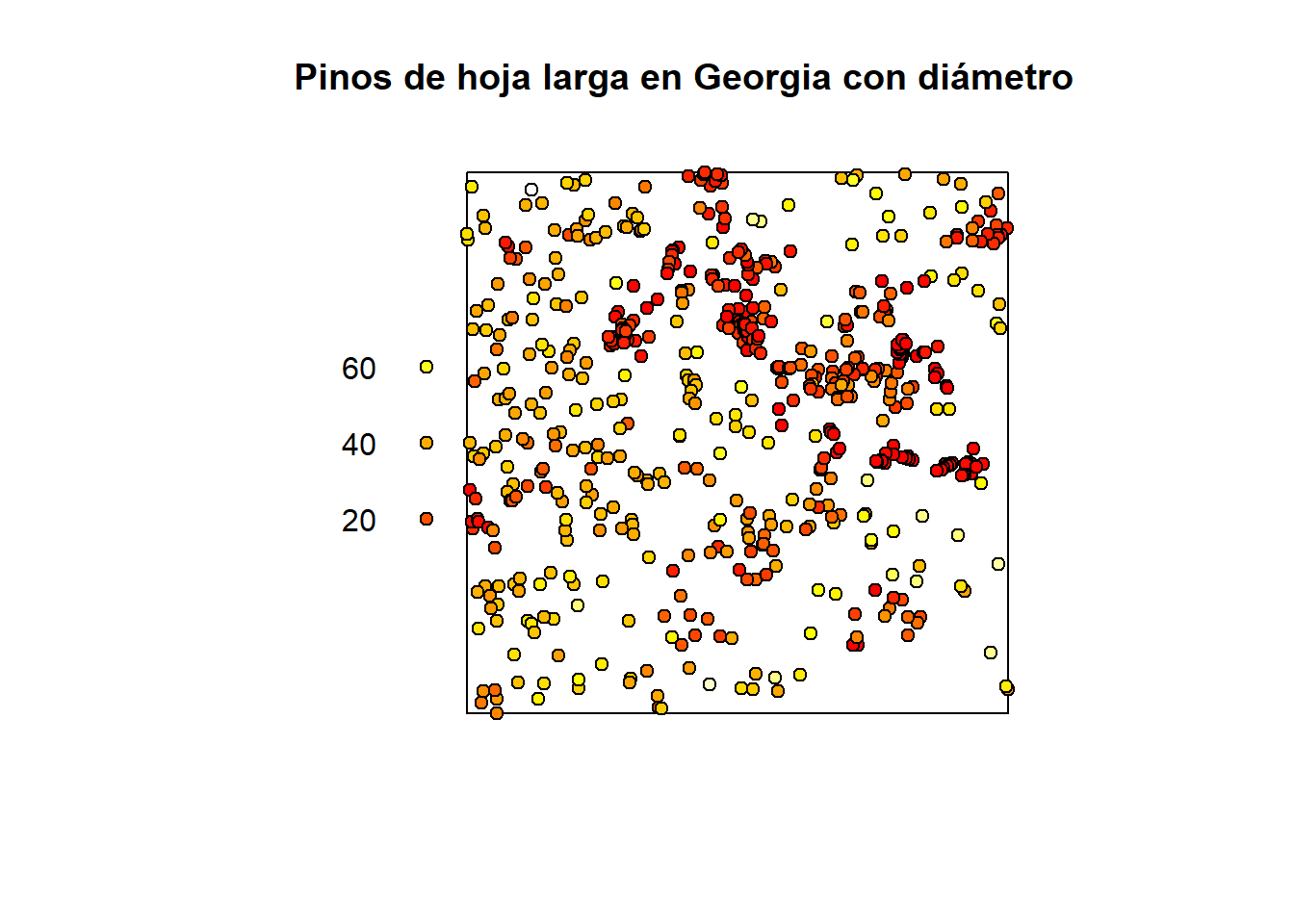

Mapa de contornos

Un mapa de contorno (o gráfico de curvas de nivel) es una representación visual de una superficie tridimensional (como una montaña, un terreno o cualquier variable continua) en un plano bidimensional. Conecta con curvas de nivel los puntos que tienen el mismo valor en una magnitud medida (altitud, temperatura, presión, etc.).

A continuación se presenta un mapa de contorno del volcán Monte Edén de Auckland.

data(volcano)
contour(volcano, 
        main = "Altitudes de Maunga Whau",,
        col = "blue", 
        lwd = 2)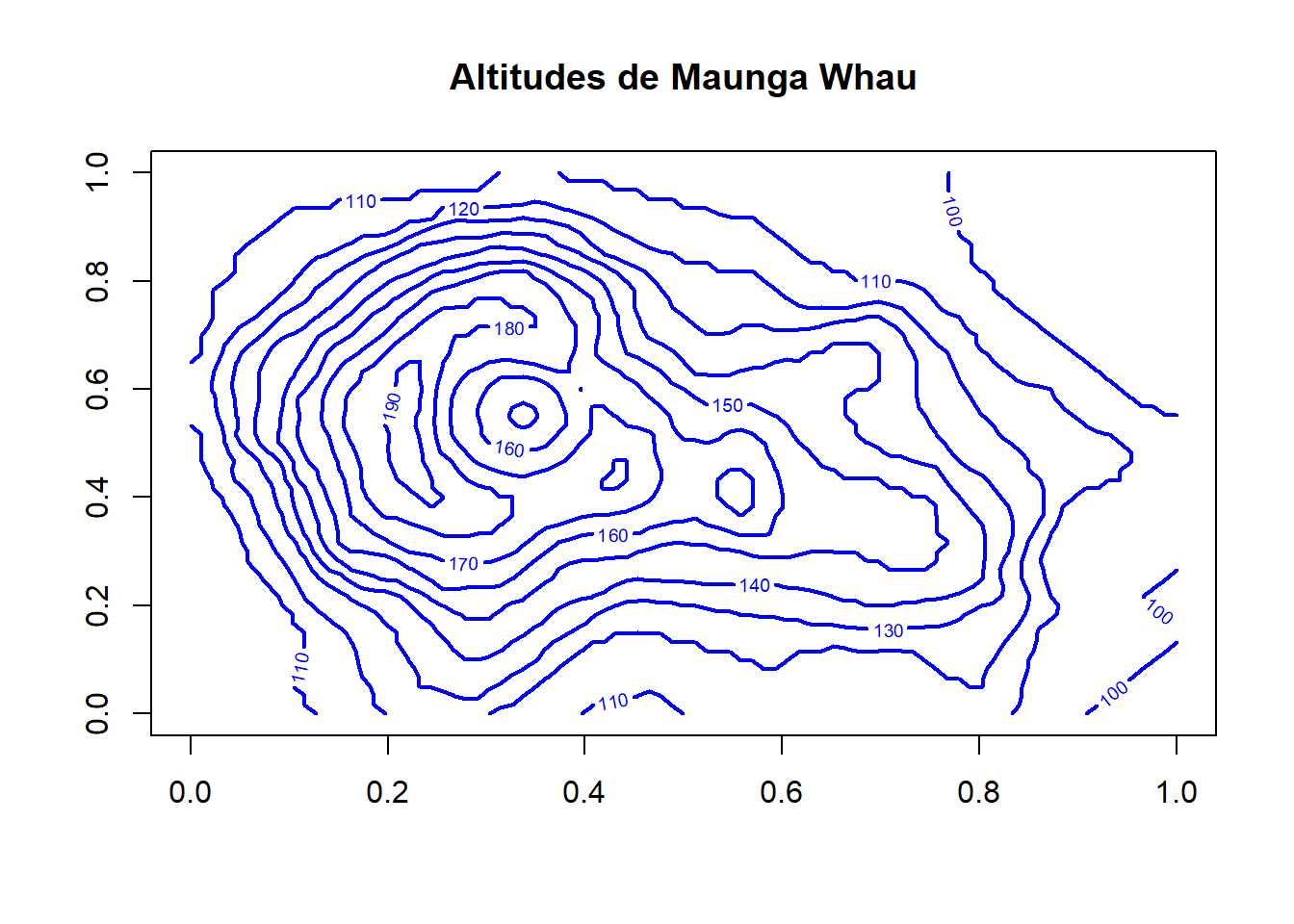

2.2.2 El variograma

Una herramienta de gran utilidad en el análisis de este tipo de procesos con estructura adicional es el variograma. La idea de este estadístico es estudiar empíricamente la estructura de covarianza del proceso espacial.

La idea se toma del contexto de series de tiempo, donde se busca medir la influencia de tiempos anteriores en el instante de estudio. Algunas de las definiciones de interés en el contexto de las series de tiempo se presentan a continuación, como se enuncian en (Rincón y De Jesús 2025).

Definición 2.6 (Estructura de covarianza y estacionareidad) Sea \(X={(X_t)}_{t\in\mathbb{Z}}\) una serie de tiempo.

1. Si \(X\) tiene media finita, la función media es \(t\mapsto\mu(t)=\mathbb{E}[X_t]\) para cada \(t\in\mathbb{Z}\).
2. Si \(X\) tiene segundo momento finito, la función varianza es \(t\mapsto\text{Var}(X_t)\) para cada \(t\in\mathbb{Z}\).
3. Si \(X\) tiene segundo momento, la función de autocovarianza es \((s,t)\mapsto\gamma(s,t)=\text{Cov}[X_s,X_t]\).
4. \(X\) es estrictamente estacionaria si para cualesquiera \(k\geq 1\) y \(\tau\in\mathbb{Z}\) se cumple que \((X_1,\ldots,X_k)\overset{d}{=}(X_{1+\tau},\ldots,X_{k+\tau})\).
5. \(X\) es débilmente estacionaria si satisface que \(\mu(t)=\mu\) y \(\gamma(t,t+\tau)=\gamma(\tau)\).
6. Si \(X\) es estacionaria, la función de autocorrelación es \(\displaystyle\rho(\tau)=\frac{\gamma(\tau)}{\gamma(0)}\).

La propiedad de ser estacionaria quiere decir que la estructura de correlación depende únicamente del tamaño del periodo que se revise y no de los instantes específicos en los que se vea el proceso, tal tamaño del periodo es la separación entre el inicio y el final del periodo. En el contexto de los datos espaciales, las nociones de estacionaridad se definen en términos de la distancia entre dos puntos.

Definición 2.7 (Proceso espacial estacionario) Sea \(Z={(Z(s))}_{s\in A\subseteq\mathbb{R}^d}\) un proceso espacial. Decimos que \(Z\) es un proceso intrínsecamente estacionario si satisface que para todos \(s,h\in\mathbb{R}^d\)

\[\mathbb{E}[Z(s+h)-Z(s)]=0\quad\text{y}\quad\text{Var}(Z(s+h)-Z(t))=2\gamma(h),\]

donde \(\gamma\) es el variograma de \(Z\). \(\gamma\) satisface que, para todos \(s_1,\ldots,s_k\in A\) y \(\alpha_1,\ldots,\alpha_n\in\mathbb{C}\) tales que \(\alpha_1+\cdots+\alpha_n=0\)

\[\sum_{i=1}^k\sum_{k=1}^k\alpha_i\overline{\alpha}_j2\gamma(s_i-s_j)\leq 0.\]

En pocas palabras, el variograma es una medida de la tendencia a ser diferentes de los valores según su distancia. Algunos comentarios que se pueden hacer a partir del variograma son las siguientes.

• Cuando \(h\) es pequeño, se espera que \(\gamma(h)\) sea pequeño, es decir, que las observaciones sean similares.
• Cuando \(h\) crece, usualmente \(\gamma(h)\) suele aumentar.
• A partir de cierto \(h_0\), usualmente para \(h\geq h_0\) se tiene que \(\gamma(h)\approx\text{cte.}\). A este \(h_0\) se le llama rango.
• Hay veces que \(\gamma(h)\to\gamma_0>0\) cuando \(h\to 0\). A este valor \(\gamma_0\) se le llama efecto nugget (por las pepitas de oro encontradas en ríos, o en inglés, los ‘’gold nuggets’’).

A continuación se presenta un estimador clásico del variograma, el cual fue propuesto por Mathéron en 1962.

Definición 2.8 (Variograma muestral) El variograma muestral del proceso espacial \(Z\) es

\[2\widehat{\gamma}(h)=\frac{1}{|N(h)|}\sum_{N(h)}{(Z(s_i)-Z(s_j))}^2,\]

donde \(N(h)=\{(i,j)\ :\ s_i-s_j=h\}\) y \(|N(h)|\) es el número de elementos distintos en \(N(h)\).

Una de las principales desventajas de este estimador es su sensibilidad a valores grandes de \(Z\). En (Cressie 2015) se puede revisar una variedad de ejemplos del uso de variograma. Aquí se da seguimiento al ejemplo del río Meuse de la sección Sección 2.1.2, presentando el variograma de los datos del plomo.

library(sp)
library(sf)
library(gstat)

data(meuse)
meuse_sp <- meuse
coordinates(meuse_sp) <- ~x + y

vg_lead <- variogram(log(lead) ~ 1, data = meuse_sp, cloud = FALSE)

plot(vg_lead$dist, vg_lead$gamma, 
     xlab = "Distancia (m)", 
     ylab = "Semivarianza",
     pch = 19, col = "red",
     main = "Variograma muestral de Plomo (log-escala)",
     cex.main = 1.2, cex.lab = 1.1)

text(vg_lead$dist, vg_lead$gamma, 
     labels = vg_lead$np, 
     pos = 3, cex = 0.8, col = "blue")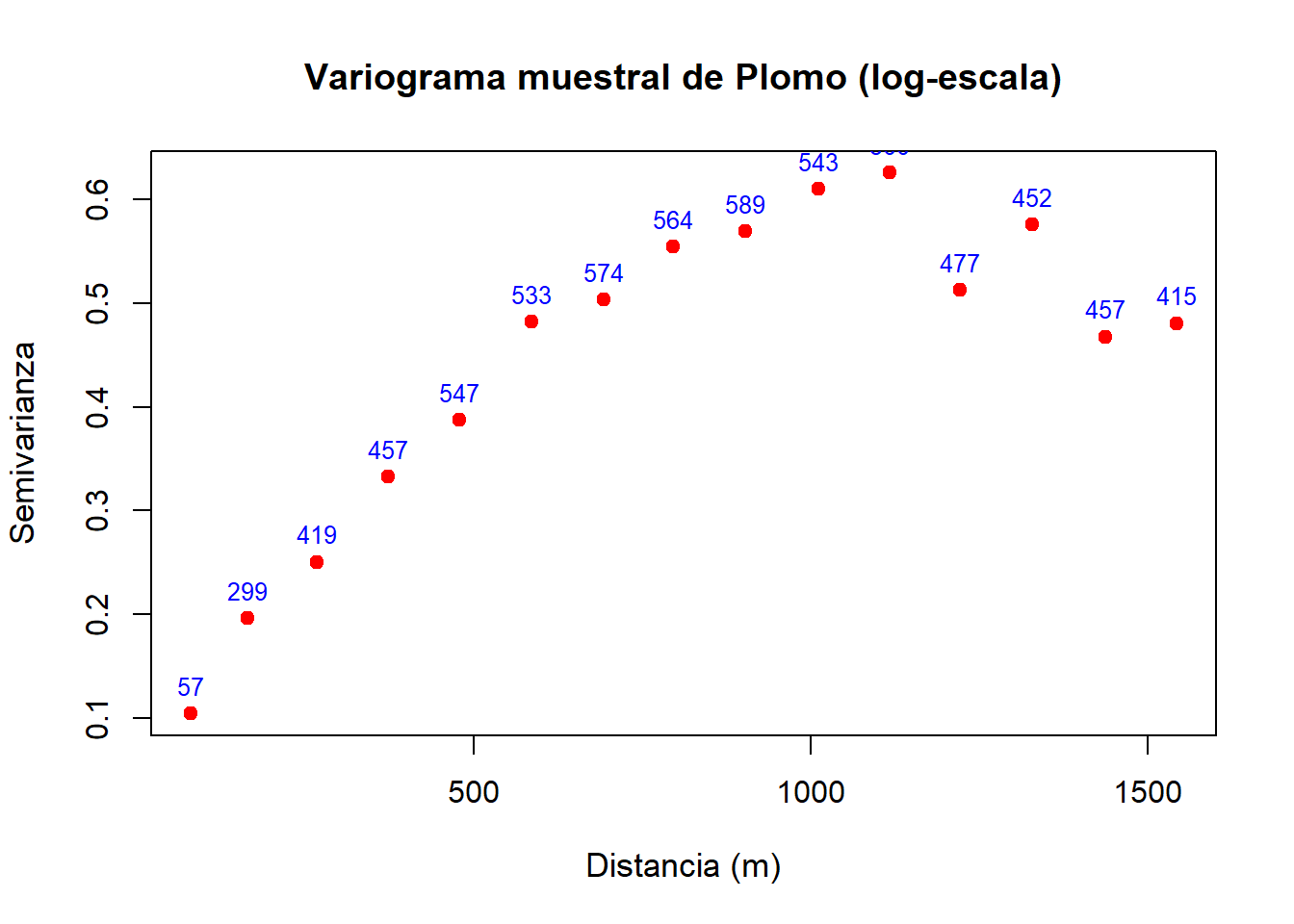

Los números sobre cada punto en el mapa representan el número de pares de observaciones de \(|N(h)|\) usados para la semivarianza. La utilidad de estos números radica en que

• Dan un criterio para medir la confiabilidad de cada punto: si un punto se basa en pocos pares, la estimación es menos confiable.
• Ayudan a evaluar la dispersión de las distancias: muchos pares en una banda significa que esa distancia es común en el diseño del experimento.

Baddeley, Adrian, Ege Rubak, y Thomas Turner. 2015. Spatial Point Patterns: Methodology and Applications with R. First. Chapman; Hall/CRC.

Bivand, Roger, Edzer Pebesma, y Virgilio Gomez-Rubio. 2013. Applied Spatial Data Analysis with R. Second. Springer.

Cressie, Noel. 2015. Statistics for Spatial Data. Revised. Wiley.

Klenke, Achim. 2020. Probability Theory: A Comprehensive Course. Third. Wiley.

Moraga, Paula. 2023. Spatial Statistics for Data Science: Theory and Practice with R. First. Chapman & Hall/CRC.

Pebesma, Edzer. 2022a. Simple Features for R. R-project.

Rincón, Luis, y Verónica De Jesús. 2025. Una introducción a las series de tiempo. First. La prensa de Ciencias.